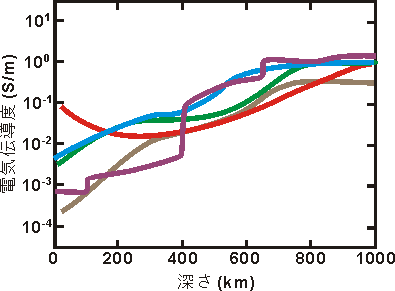
図１　マントルの電気伝導度観測モデル
紫線：太平洋北部、青線：中国東北部、茶線：カナダ楯状地、緑線：アメリカ合衆国南西部、赤線：ハワイ

注：　S/mは電気伝導度の単位。S (ジーメンス)は電気抵抗の逆数で、Ω^-1に等しいです。S/mは1m×1m×1mの立方体の電気伝導が1Ω^-1であることを意味しています。


Krocker-Vinikの記号

　鉱物の電気伝導度にとって格子欠陥は本質的に重要なので、鉱物の電気伝導度について議論する前に、
格子欠陥を表すKrocker-Vinikの記号について簡単に説明しようと思います
　まず、基本となる部分は、欠陥の種類、つまりイオン・電子・空孔を表します。イオンは元素記号で表しますカンラン石とその高圧相の場合、Mg・Fe・Si・Ｏです。電子と電子空孔は、それぞれ e と h で表します。結晶席にあるべきイオンが抜けているものを空孔と呼びますが、Vで表します。下付き文字は、結晶席を表します。カンラン石とその高圧相の場合、Mgサイト・Siサイト・Ｏサイトとinterstitialです。interstitial は I で表します。上付きの・と′は正と負の過剰電荷を表します。過剰電荷がないときは上付きxを付けます。従って、通常のサイトにいるMg²⁺, Si⁴⁺, O²⁺ イオンは、Mg_Mg^X,，Si_Si^X ， O_O^X と表します。MgサイトのFe²⁺イオンは、過剰の電荷を持っていないのでFe_Mg^x と表し、Fe³⁺イオンは、過剰の性の電荷を持っているのでFe_Mg^・と表します。電子と電子空孔は、それぞれ負の電荷と性の電荷を一つ持っているので、e′と h^・で表します。Mgサイト・Siサイト・Oサイトの空席は、V_Mg`` and V_Si```` and V_O^??,と表します。小さなイオン、特に水素イオンは、正規の結晶席以外のところに割り込んでいることが多いのですが、それはH_I^?と表します。


鉱物の電気伝導度メカニズム

　マントルの主要構成鉱物は金属ではないので、電荷は必ずしも自由電子で運ばれるわけではありません。ここでは、マントル主要構成鉱物で重要であろうと予想される電気伝導メカニズムについて解説します。

小さいポーラロン伝導
　マントルの構成鉱物の多くは、かなりの量のFeを含んでいます。従って、Fe²⁺からFe³⁺への電子のホッピングがもっとも有力な電気伝導度メカニズムと考えられます。電子がジャンプするにはエネルギー障壁E_hを越えないといけないので、電気伝導度σは、通常次のように表されます。
　σ = σ₀ exp[-E_h/k_bT]　　　　　　　　　（１）
ここに、σ₀はボルツマン定数、Tは絶対温度です。指数係数σ₀は定数とみなすことが多いですが、温度の関数であり得ります。エネルギー障壁は活性化エネルギーと呼ばれます。電子のホッピングの活性化エネルギーE_hは非常に小さく、0.1～0.2eV程度と考えられています。
　電子のホッピングは、見方を変えると、下図に示されるようにFe_Mg^・の移動と考えることが出来ます。
　
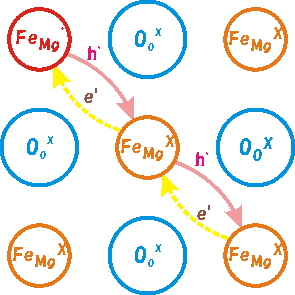
図２　電子ホッピングによる電気伝導

　しかし、過剰の正の電荷を持つイオンが存在すると、陽イオンは反発し、陰イオンはひきつけられて、結晶格子がゆがみます。これを小さいポーラロンと呼びます。

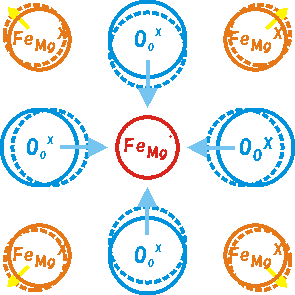
図３　小さいポーラロン。Fe_Mg^・の正の過剰電荷によって、正の電荷を持つFe_Mg^xは正規の位置より斥けられ、負の電荷を持つ O_O^Xはは正規の位置より引き寄せられる。

　Fe_Mg^・が移動すると、この格子のひずみも移動します。格子のひずみも一緒に移動するため、エネルギー障壁は、電子の移動のみで考えるより遥かに大きくなります。小さいポーラロンによる電気伝導度も、(1)式と同じ形で書けて、
　σ = σ₀ exp[-E_p/k_bT]　　　　　　　　　（２）
ここに、E_pは小さいポーラロンの活性化エネルギーです。上記の理由で、E_p>> E_hで、0.5eVから2eVぐらいの値になります。電気伝導度は温度と共に上昇します。
　小さいポーラロン伝導では、電荷はFe_Mg^・で運ばれるので、電気伝導度はFe_Mg^・とFe_Mg^xの数の関数となります。従って、鉱物の鉄の含有量が増加すると、電気伝導度は増加します。また、系の酸素分圧が上昇すると、Fe2+が酸化されて、Fe3+（Fe_Mg^・）が増加します。従って、系が酸化的だと電気伝導度は上昇します。
　高圧では、鉱物は圧縮されてエネルギー障壁の高さが変化します。活性化エネルギーに圧力効果を加えたものを、活性化エンタルピーHと呼びます。
　H = E + PV　　　　　　　　　　　　　　　　　（３）
　ここにPは圧力で、Vは活性化体積と呼びます。小さいポーラロン伝導の場合、原子間距離が縮まるために、電気伝導度は圧力と共に上昇すると期待されます。すなわち、活性化体積は負です。しかし、圧力効果は小さいようです。

イオン伝導
　イオンは電荷を持っているので、イオン自体が移動することにより、電荷を運ぶことが出来ます。これをイオン伝導と呼びます。マントルの主要構成鉱物の場合、イオンが移動するためには、隣の結晶席が空であることが必要です。これを逆に見ると、下図に示されるように、空孔が移動していると見ることが出来ます。マントル主要構成鉱物では、通常Mg席のイオンが一番動きやすいので、V_Mg''を例にとっています。

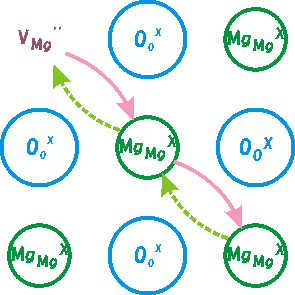
図４　イオン伝導。空孔V_Mg``の移動により、電荷を輸送する。

　原理的には、V_Si''''やV_O^・・も電荷を運びうるのですが、SiやOのイオンの動きやすさ（拡散係数）はMgよりずっと低いので、これらの空孔は実質的に電気伝導に寄与しません。
　イオン伝導による電気伝導度も（１）・（２）と同様の式で表せます。
　σ = σ₀ exp[-E_i/k_bT]　　　　　　　　　（４）
E_iはイオン伝導の活性化エネルギーです。イオン伝導では、イオンが他のイオンを掻き分けて移動しなければならないので、活性化エネルギーは非常に大きく、通常、E_i>>2 eVです。これは、式（３）から、イオン伝導は高温で卓越する電気伝導メカニズムであることを意味しています。
　電荷をバランスさせるために、Fe_Mg^・が増加すると、V_Mg''も増加します。従って、小さなポーラロン伝導と同じように、鉄の含有量と酸化状態が高くなると、イオン伝導も増加します。
　圧力が上昇すると、原子間距離が縮まり、イオンは動きにくくなります。従って、イオン伝導による電気伝導度は圧力と共に減少すると期待されます。すなわち、活性化体積は正です。

プロトン伝導
　水素イオンは小さいために、拡散係数が著しく大きいので、ごく少量でも水素が存在すると、鉱物の電気伝導度に大きな影響を与える可能性があります。H_I^・による電気伝導をプロトン伝導と呼びます。マントル鉱物は、高圧下では水を含みうる鉱物がありますので、それらではプロトン伝導は重要な電気伝導メカニズムになる場合があります。

熱起電力
　電気伝導度メカニズムを特定することは容易ではありません。電気伝導度を特定するために有用な情報は熱起電力です。高温では、電荷移動を担う粒子（キャリアと呼びます）が激しく動き回るので、試料内に温度差ΔTが存在すると、その温度差に応じた電圧ΔVが発生します。電圧と温度差の比の逆符号を、熱起電力Qと呼びます。
　Q = - ΔV/ΔT 　　　　　　　　　　　　　　（５）
熱起電力の符号は、卓越する電気伝導キャリアの符号を示しています。


マントル鉱物の電気伝導度

１．カンラン石
　カンラン石の電気伝導度は広く研究されています。熱起電力の測定では、低温ではキャリアの電荷は正で、高温では負であることが示されています。従って、電気伝導度メカニズムは、最低２種類あることが分かります。低温で卓越するメカニズムはFe_Mg^・の小さいポーラロン伝導で、高温ではV_Mg''のイオン伝導であると考えられています。ある論文では、鉄マグネシュウム比Mg/(Mg+Fe) = 0.91、酸素分圧が10-4 Pa、圧力一気圧のカンラン石の電気伝導度は、
　 σ = 10^2.4 (S/m) exp [-1.6 (eV) /k_bT]] + 10^9.2 (S/m) exp [-4.2 (eV) /k_bT].　　　　（６）
と なっています。第１項が小さいポーラロン伝導で、第２項がイオン伝導です。イオン伝導の活性化エネルギーは4.3eVと、小さいポーラロン伝導の活性化エネルギー1.6eVより大分大きいです。
　小さいポーラロンによるの電気伝導度は、Fe/(Mg+Fe)の1.8乗に比例して大きくなります。また、酸素分圧の1/７乗に比例して大きくなります。圧力依存性は小さく、活性化エネルギーは正で0.6 cm³/molという報告があります。活性化エネルギーが正であるのは、小さいポーラロンモデルと矛盾します。
　カンラン石は斜方晶系なので、電気伝導度も異方性があることが予想されます。報告では、[001]方向の電気伝導度は、[100]方向や[010]方向の電気伝導度の約２倍だと言われています。
　カンラン石の化学組成は、一般的にM₂SiO₄という化学式で表されます。ここに、MはMg, Fe, Ni, Caなどの２価の陽イオンです。けれども、高圧では最大1000ppm程度の少量のH⁺イオンがカンラン石の結晶構造中に入り込むことが出来ます。H⁺の拡散係数は非常に大きいので、この少量のH⁺イオンによって電気伝導度がもっと高くなる可能性がありますが、実験的には確かめられていません。

２．ワズレアイトとリングウッダイト
　リングウッダイトはスピネル構造をとっています。即ち、１対のMgO6八面体の構造単位AとSiO4クラスター構造単位Ｂが交互に積み重なった構造をとっています。ワズレアイトは、スピネル構造に類似した変形スピネル構造をとっています。ここでは、構造単位AとBが二つずつ、即ちAAとBBが交互に積み重なった構造となっています。このように、この二つの鉱物は非常に似た構造をとっており、その物性値は非常に良く似ています。電気伝導度も両者は良く似ています。その電気伝導度は、活性化エネルギーFe_Mg^・の小さいポーラロン伝導であると考えられています。活性化エネルギーはカンラン石より小さく、1eV程度です。即ち、この二つの鉱物の電気伝導度の温度依存性は非常に小さいです。
　ワズレアイトの電気伝導度は、マントルに相当する温度では、カンラン石より二桁ほど高い値となっています。従って、カンラン石－ワズレアイト転移に対応すると考えられている410km不連続では、電気伝導度は大きくジャンプすると考えられます。リングウッダイトの電気伝導度は、ワズレアイトより少し高い程度です。従って、ワズレアイトーリングウッダイト転移に対応すると考えられる520km不連続では、電気伝導度のジャンプはきわめて小さいといえます。
　ワズレアイトとリングウッダイトは、ケイ素を置換することにより、最大3%の水を含むことが出来ます。ワズレアイトやリングウッダイトの高電気伝導度は、中に含まれる水のせいではないかという意見もありますが、良くわかっていません。

３．ペロフスカイト
　下部マントルを構成するペロフスカイトの組成は、第一近似で(Mg,Fe)SiO₃ですが、この成分に加えてAl₂O₃成分を含むことが出来ます。下部マントルでは、ペロフスカイトは6％のAl₂O₃成分を含んでいると考えられています。ペロフスカイトのMgサイトはAlにとっては大きすぎるので、Alは主にSiのサイトを置換します。その結果、電荷を保つために、Alを含むペロフスカイトのMgサイトのFeは3価であると考えられています。
　Alを含まない(Mg_0.9Fe_0.1)SiO₃ペロフスカイトの電気伝導度は、1400℃から1600℃で10^-0.8S/mから10^-0.5S/mで、3%のAlを含む(Mg_0.9Fe_0.1)SiO₃ペロフスカイトの電気伝導度は、同じ温度範囲で10^-0.3S/mから10⁰S/mと、半桁高くなります。このことから、主な電気伝導度メカニズムがFe_Mg^・の小さいポーラロンであることが推定されます。Alを含むペロフスカイトも含まないペロフスカイトも、活性化エネルギーは0.6eVから1.0 eVで、ワズレアイトやリングウッダイトよりなお小さな値となっています。

  下部マントル最上部でのペロフスカイトの電気伝導度は、10⁰ S/m程度であり、リングッダイトより半桁ほど高い値です。従って、660km不連続では電気伝導度の跳びが存在するはずです。けれども、カンラン石ーワズレアイト転移では２桁増えますから、410ｋｍ不連続での跳びの1/4程度と予想されます。
　ペロフスカイトの電気伝導度の圧力依存性は非常に小さく、その活性化体積は約 -0.1 cm³/moleであることが知られています。この小さな負の活性化エネルギーは、小さいポーラロンモデルと矛盾しません。マントルの温度勾配は0.2-0.5 ℃/kmと非常に小さいと予想されるので、活性化エネルギーが小さいこともあって、下部マントルの電気伝導度はほぼ一定と予想されます。

４．マグマ
　ケイ酸塩融体（マグマ）は、固体より高電気伝導度です。1200℃以上で、電気伝導度は10⁰ S/mから10² S/mの範囲にあります。マグマの電気伝導度が高いのは、マグマ中のイオンの易動度が大きいためだと考えられます。即ち、マグマの主要な電気伝導度メカニズムは、イオン伝導と予想されます。
　マントル深部では、マントル岩中でのマグマの濡れ角は非常に小さいので、割合が小さくても簡単にネットワークをつくると予想されます。マグマのネットワークは電気伝導の道となるので、少しでもマグマが存在すれば、電気伝導度は大きく上昇すると予想されます。上部マントル最上部に高電気伝導度層が存在するのは、この領域で少しですが部分融解が起きているためである可能性があります。


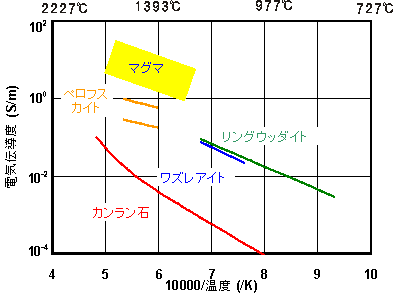
図５　マントル鉱物の電気伝導度のまとめ。横軸は、絶対温度の逆数の１万倍。縦軸は、電気伝導度の常用対数。これをアーレニウスプロットという。電気伝導度がアーレニウスの式（式１、２、４）で表されるとき、上の図では直線となる。カンラン石の電気伝導度は、曲線となっていることに注意。


マントルの電気伝導度分布の解釈

　実験室で測定して決定したマントル鉱物の電気伝導度から推定したマントルの橄欖岩の電気伝導度プロファイルを、第１図に重ねたものを第６図として下に示します。一般に、より高圧条件で安定な鉱物は、より高電気伝導度です。このことが、上部マントルで深さと共に電気伝導度が上昇する理由と考えられます。また、より高圧の鉱物は、活性化エネルギーが小さいといえます。このことが、上部マントルでは電気伝導度の地域性が大きく、下部マントルで電気伝導度の均質性が高い理由と考えられます。
　地震学的660km不連続や410km不連続のジャンプは両方とも大きいです。しかし、、電気伝導度のジャンプはカンラン石－変形スピネル転移の方がポストスピネル転移より４倍大きいので、もしちゃんと観測できたなら410kmの方が660kmよりずっと大きいと予想されます。
　上部マントル最上部の高電気伝導度層は、通常のカンラン岩の電気伝導度では説明できません。別の電気伝導の寄与が必要です。一つの説明は、この領域で部分融解が起こり、マグマが電気伝導の道を作っているというものです。もう一つの説明は、この領域のカンラン石が水素をある程度含み、プロトン伝導によって電気伝導度が増加するというものです。現在のところ、実験的証拠がないので、どちらが正しいのか分かりません。

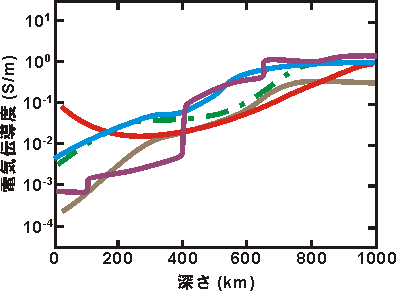
図６　マントルの電気伝導度観測モデル
黒線：　鉱物学的モデル、紫線：太平洋北部、青線：中国東北部、茶線：カナダ楯状地、緑線：アメリカ合衆国南西部、赤線：ハワイ


参考文献

• Poirier, J.-P., Introduction to the physics of the Earth’s interior, 2nd edition, Cambridge Univesity Press, Cambridge, pp. 312, 2000.
• Xu, Y., T.J. Shankland, and B.T. Poe, Laboratory-based electrical conductivity in the Earth's mantle, J. Geophys. Res., 105 (B12), 27865-27875, 2000.
• Utada, H., T. Koyama, H. Shimizu, and A.D. Chave, A semi-global reference model for electrical conductivity in the mid-mantle beneath the north Pacific region, Geophys. Res. Lett., 30 (4), 1194, doi:10.1029/2002GL016092, 2003.