| 高温高圧実験に対する有限要素法解析の応用 | 米田 明 | ||
|---|---|---|---|
| 有限要素法は偏微分方程式で記述される現象すべてに応用可能です。シュレンジンガー方程式も有限要素法で解くことができます。高温高圧実験においては、応力場の解析にも温度場の解析にも使えます。装置の設計はもちろん、地球科学の諸問題、電磁気現象、化学反応場などの解析にも使えます。もし有限要素法をマスターできれば、それまで手に負えなかった問題に明確な指針を得ることができます。是非トライして頂きたいです。 | |||
 |
本解説は最近の学会発表でのパワーポイントのスライドに沿っています。 三つの話題を紹介しています。最初のものは高圧発生原理の入門ともいうべきもので年配の研究者にとっては常識ですが、若い人たちには認識されてないのではと危惧しているので取り上げました。二番目は実際の研究での応用例です。実験や解析の過程で近似や仮定が導入されますが、その妥当性を有限要素法で確認しました。最後の話題は筆者が目下取り組んでいるものです。ガスケット材の弾性変形だけでなく塑性変形を取り扱う点で難易度の高い課題です。従って現在“工事中”であり、ここでの解説は割愛します。 |
 |
左図は筆者が使っているソフトウェアFEMLAB3です。最近COMSOLに名称変更されたようです。20年ぐらい前は、有限要素法解析を貫徹するためには多大な時間と労力を要しました。今では、後で示すように、ものすごく簡単にできるようになっています。先人達の努力の賜物です。 このソフトは、もちろん習得には少し時間がかかりますが、極めてユーザーフレンドリです。最近のこのソフトの特徴としてオンラインヘルプも充実しています。英語ですが、この程度英語は読みこなしてほしいところです。 ただ、このソフトを使用する前に、有限要素法について少しは勉強して頂きたいです。但し要点だけで十分ですから、なるべく薄くて簡単そうな、参考書“****入門”で十分です。ちなみに筆者が読んだのは“有限要素法への入門(戸川隼人著、 170ページ、サイエンス社)”だけです。古い本なので今は入手困難かもしれません。 先述したガスケット材の弾塑性変形解析を実施するにあたり、要素間のオーバーラップの問題が生じました。 この問題解決のためCOMSOL社のサポートに連絡したところ、次のバージョンで対策を講じてもらえました。ユーザーのニーズに迅速に対応してくれますので感謝しています。 |
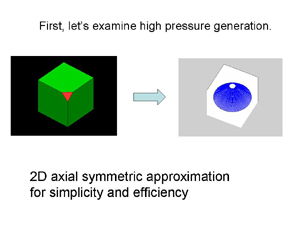 |
川井型装置における立方体アンビルを、円錐型アンビルで近似します。COMSOLでは3次元解析も可能ですが、とりあえず、円錐近似でも本質的な事柄は押さえられるはずです。 |
 |
デモンストレーションの意味もありますので、これからやる解析の時間を計測することにしました。早く終わりたいので、邪魔が少ない日曜日に行いました。 このようなことは研究そのものではないですが、学会発表では結構ウケるのです。またCOMSOLでの有限要素法にかかる手間や時間についての大体の印象を持ってもらう効能もあるのです。 |
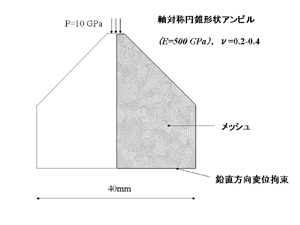 |
マッシブサポート効果解析の条件です。絵をかいてメッシュ切り境界条件を入れるだけです。こういう操作がワンタッチでできるようになっています。20年ほど前に有限要素法をかじったころとは雲泥の差です。20年前に卒論研究として例題解析をやらせたのですが、境界条件の入力が面倒で結局学生が卒業し中断してしまいました。 |
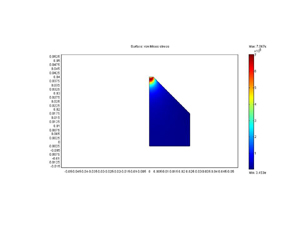 |
解析の結果です。発生圧力10GPaに対し、アンビル内の最大差応力は約7GPaです。つまりアンビル材の材料強度より4割ほど高い圧力が発生できることを示しています。つまりアンビル先端を取り囲む周辺部が先端部をサポートしているわけです。これが所謂マッシブサポート効果であり、日本語で
“質量支持効果”と呼ばれることもあります。 仮に使用する超硬合金の圧縮強度が7GPaであれば、ブリッジマンアンビル装置で10GPaは、マッシブサポート効果で発生できるわけです。それ以上の圧力発生はもっと積極的にラテラルサポート(ガスケットによるアンビル側面の締め付け)を行う必要があります。ブリッジマンアンビル装置にラテラルサポート効果を導入したものがドリッカマー装置です。 |
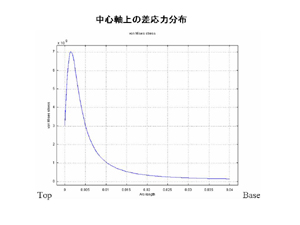 |
アンビル中心軸上の差応力分布図です。左側がアンビル先端、右側がアンビル底面になります。先端から少し内部に入ったところで差応力が最大になります。つまりアンビルの破壊はその辺から進行する可能性が最も高いわけです。この結果は弾性論に基づく解析解とほぼ一致します。但し解析解ではアンビルを半無限弾性体と近似しますので、アンビル側面の傾斜の効果を見積もるには有限要素法解析が不可欠となる。 |
 |
先ほどのスライドの結果を得るまでに僅か24分でした。COMSOLでの有限要素法にかかる手間や時間についての大体の印象を持ってもらえるでしょう。 |
 |
COMSOLだけですと単一の条件の解析しかできません。少しずつ条件を変えた一連の解析を行うには不便ですが、MATLABとのコンビネーションで使うことにより解決します。COMSOLにはMATLABソースファイルでセーブする機能がついています。ある条件でCOMSOLの解析が終われば、その条件をMATLABソースファイルでセーブし、自分が変更したいパラメータを編集し、forループで回せば一括解析できます。 MATLABも高価なソフトですが、最近COMSOL社は“COMSOL Script”を売り出しています。これはほとんどMATLABと同じです。 MATLABを持っていない方には、少し追加料金を払って“COMSOL Script”の購入をお勧めします。 |
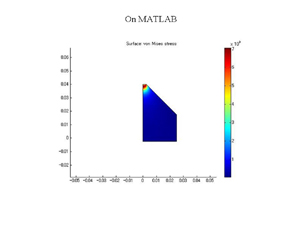 |
同じ解析をMATLABでやった場合の解析結果の図です。条件を少しずつ変えて繰り返し計算する場合は、MATLABに移行した方が楽です。 COMSOLファイルからMATLABファイルへの変換もワンタッチです。 |
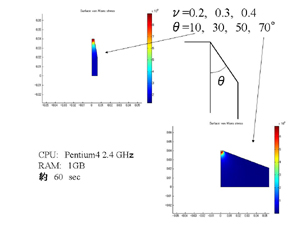 |
アンビルの傾斜角とポアソン比を変数にしてみました。次のスライドで結果を見せます。使用したパソコンは特別仕様ではなく、一般的なものです。 |
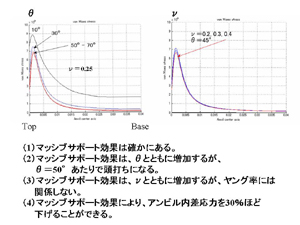 |
結果のまとめです。この解析で得られる結論はスライド中に(1)-(4)でまとめてあります。 一昔前なら、これでも十分卒論研究になったと思われます。こんなに簡単になってしまうと、そういうわけにはいきませんが。 |
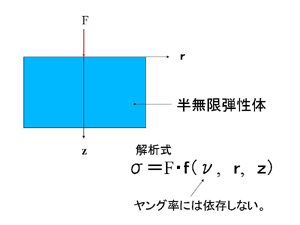 |
前スライドの結果は有限要素法解析をやる前から予想できます。弾性論(例えばTimoshenko and Goddier)の教科書には上記のような場合の解析解が載せられています。 ちなみに半無限弾性体での有限要素法による数値解は解析解と完璧に一致しています。 |
 |
というわけで4時間弱で終了です。実は途中で邪魔が入って一時間ほど中断したので、実質3時間の労働でした。 |
 |
ここからは熱・温度解析に移ります。大迫氏との共同研究です。大迫氏の実験では試料端の温度一定や熱流の一次元性などの仮定が必要です。これらの仮定が十分に満足されているかどうかを有限要素法解析で確認しました。先に結論を言えば“OK”です。 大迫氏による熱伝導実験の概要は、 M. Osako, E.Ito, A. Yoneda: Simultaneous measurements of thermal conductivity and thermal diffusivity for garnet and olivine under high pressure, Phys. Earth Planet. Int., 143-144 , 311-320, 2004. を参照下さい。 |
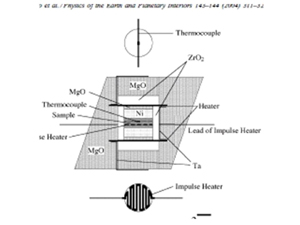 |
熱伝導実験用のセル断面図です。インパルスヒータはエッジングで製作したもので実際のものはもっとジグザグしています。このインパルスヒーターの一様発熱性も有限要素法でチェックしています。各部品については次の図を参照下さい。 |
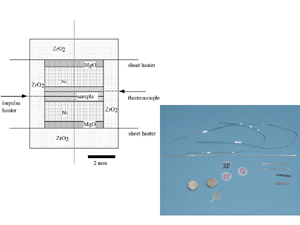 |
熱伝導実験の核心部の断面図と部品の写真です。上下のシートヒーターで高温を発生します。同じ厚さに調整された3枚の試料を使います。二つの試料間境界のうち、下の方の境界面に入れたインパルスヒーターで熱パルス(温度擾乱)を発生させます。インパルスヒーターの通電時間は僅かなのでサンプル全体の温度には影響しません。熱パルスは、上の試料間境界にいれた熱電対でモニターされます。熱電対の応答(温度のこと)を解析することにより、熱拡散率と熱伝導率が同時に測定できます。両者の比から試料の比熱を求めることができます。 |
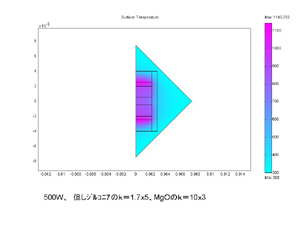 |
まずはディスクヒーターの温度分布の推定をします。試料部の温度の一様性を評価しました。詳細は次の図で示します。 |
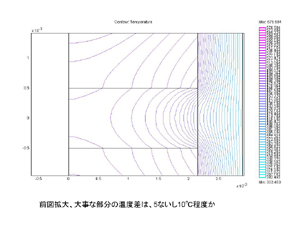 |
ジルコニアスリーブの効果により、温度均一性が良好なことが確認できました。 |
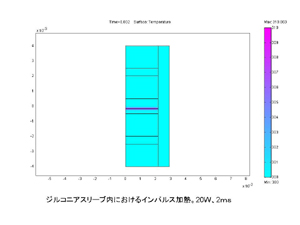 |
次にインパルスヒーターによる加熱の解析を行います。上の図はインパルス加熱の様子を示したものであり、詳細はこれより順に示していきます。 |
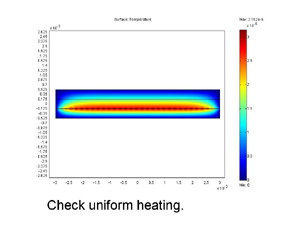 |
細線ヒーターによる均等発熱性のチェックです。今回のディメンジョンでは一様発熱とみなせます。 |
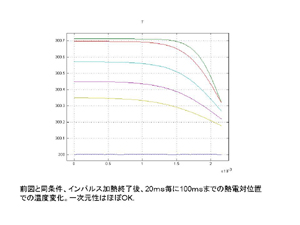 |
インパルスヒータによる熱パルスの時間依存性を表した図です。詳細はスライド下部に示しました。 |
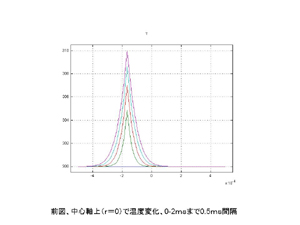 |
試料中心軸上でのインパルスヒータによる発熱の様子です。このような時間変化も解析できます。 |
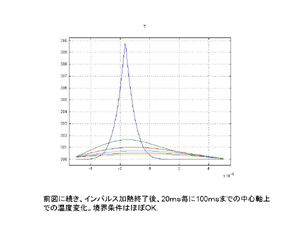 |
試料中心軸上におけるインパルス加熱終了後の温度変動です。左側での定温性は良くありませんが、熱電対に近い左側の定温性は十分確保できています。 |
| 以上示したように有限要素法は弾性変形や温度場などの数値解析に威力を発揮します。実験条件の設計のみならず、実験結果の解釈にも応用可能です。有限要素法の習得には少し時間がかかりますが(運転免許取得程度か)、一旦習得できれば研究上の様々な局面で活用できるでしょう。 | |||
| top | メンバー | 研究方針 | 学生の方々へ | 設備 | 業績 | レビュー | リンク |